TA的每日心情 | 开心
2018-8-8 03:13 |
|---|
签到天数: 1 天 [LV.1]初来乍到
|
本帖最后由 喬治兄 于 2020-1-31 16:20 编辑 1 m; Z5 o& A8 M( E4 b/ A
8 h) M$ I" X6 [! x6 f5 f
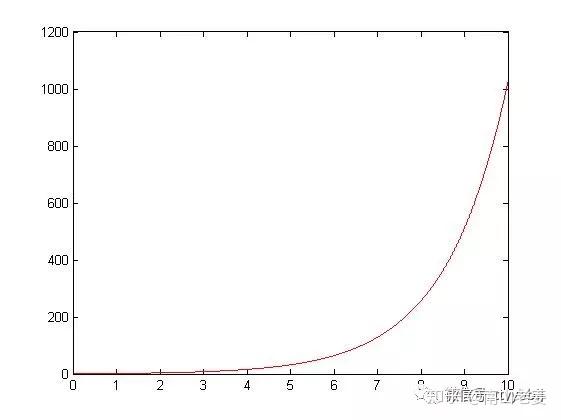
當問題的根源是呈指數型增長時則是非常嚇人的) y: @6 V4 H+ j2 [! u% V. L( P. R0 A
9 b' o' b6 }( ]. {如同高利貸的複利, 當你想付時往往為時已晚了.....+ k5 n1 t) K: h% s' {
付不起了...........8 \ H4 s* S; y8 p
5 F5 o! ~5 a. f9 J$ h3 q1 M指數型增長.....到一定程度是無法解決的.........
' Z3 A. t! h6 D! |$ R8 u3 n; o1. 因為人力, 物力, .....各項資源投入去處理指數型的問題均是龐大到不可能....2 \$ P2 u! E1 t( j
且一切的資源也不太可能是在時間許可的範圍內無限和即時供應上......# a3 T4 U% q& t/ V! U2 j* s/ j' |
2. 時間, 當指數型的問題增長因子是時間的話.......時間量度增長是很短很緊迫
- T8 s- y% _5 Y2 A$ \ 則處理指數型的問題則往往是迫在眉睫........或者早已來不及處理了......
" f$ x( ]* I l/ r' o, G3 N1 k9 y6 m6 C3 F+ v* y @
 # D" h$ E" r% c6 v# d9 n v # D" h$ E" r% c6 v# d9 n v
- Z( P) ~+ |0 [8 i$ s' l( h解說:
; _: B. v2 Z6 ~. \3 U 越到後面爬升的斜率越來越大的增長, 也將導致所有的後勤資源追不上問題增長的速度* I& i7 b0 K1 R& X5 k
( R4 d5 u. C3 |6 I# T/ J9 e7 Z
 ; \' N5 s1 q E' x6 ?* N" s) Y" Q' N. r ; \' N5 s1 q E' x6 ?* N" s) Y" Q' N. r
1 T- k# L0 c7 t& C
問題也很容易解,隔離算是最快速阻斷增長的方法
6 I$ T( p( I h/ ? x) w0 _增長因子是時間...在空間條件許可下只能用空間換取時間
9 g; o F6 W$ k+ h歷史上不乏類似此類緊急危機事件的發生+ r# f; _/ u5 B |5 }- j
當事件發生時一般也不太可能即時找到正確的處理方法來對症下藥- S6 y* b7 L2 @9 E4 r* u6 M8 [
+ {4 g$ d- C" h隔離阻斷,堅壁清野,各個擊破.....既能治標又能治本....標本兼顧
. {; a: _0 P9 f
4 f: ]6 r" m3 S& D% D: b" o 3 _0 u3 ]2 p- _5 x 3 _0 u3 ]2 p- _5 x
, Q: l4 o: B# W, R8 _
轉載......
; J/ q" M. z/ nhttps://zhuanlan.zhihu.com/p/57999354& @5 k( {+ T5 m: ]
+ K0 k' g1 h& j
指数增长与成长问题
0 s9 v. e. @$ G1 c5 e) _: ~
1 v2 I' ^! V) r9 H- n3 x0 L! V南山老姜
?8 s+ K* b6 N T2 [ u8 D' {( ?% u& h C g6 ^
" B1 B/ t# K3 L一个思考践行自己和儿子成长的父亲【公众号:跬步成长事业】
( f. P5 G3 s2 U0 F, L2 U
+ a; X1 i. I* z' M# X5 j
5 }# X2 g$ \# w4 z+ G: y7 y
7 Z" i& E3 \7 V' A V x, `3 T/ O( b& m% I2 x- C$ B8 G* p
# t( O, k% W& v8 B5 g5 Y" B
4 N# R" N- x# i. T2 a' ]/ V$ Y
' ^; e- e s/ U$ I- r; w1 j, t5 Y1 ?$ X( k* X
4 ^- l5 r3 i4 H+ N- H V
, q6 ~+ ~7 }2 J! S/ m: R D2 l, p+ c# {& b7 g; }
1 L, ~3 O4 C# `5 g6 g8 F: X6 L
# V& q8 j9 Y5 m/ j4 V8 `# e9 P7 A' m( s/ x4 {; r5 V# J( p
上周在《系统思考》一书中看到一个青蛙与睡莲的小故事,道理很深刻。 一群青蛙幸福地生活在一个大池塘的一角,池塘的另一边是一片睡莲。它们的生活是如此平静恬适,相安无事。一天,池塘里面流进了一些刺激睡莲生长的化学污染物,它们可以让睡莲每24小时增长一倍。这对青蛙而言是个问题,因为如果睡莲覆盖了整个池塘,它们就将无处容身了。如果睡莲可以在50天内覆盖整个池塘,而青蛙有一种阻止睡莲生长的方法,但是需要花10天时间来将这个方法付诸实施。那么,问题来了:什么时候池塘会被覆盖一半?问在池塘被睡莲覆盖的面积达到多少时,青蛙才有可能采取行动去挽救它们自己? 仔细分析这个小故事里,会发现其中隐含着的让我们吃惊的深刻道理。 第一个问题很简单,如果睡莲50覆满池塘,而且它们每天增长一倍,那么第49天结束的时候,池塘就将被遮盖掉一半——而不是在第25天。因为这种增长是指数级增长,而不是线性增长。 第二个问题指出,青蛙们可以阻止睡莲的增长,但是需要l0天时间才能完成这项工作。因此,它们则最迟要在第40天结束之前开始行动。那么,第40天的时候池塘会被睡莲覆盖掉多少呢?解决这个问题的最简单方法就是倒推。我们知道,到第50天结束时,池塘会被睡莲完全覆盖;第49天,池搪将被覆盖l/2;第48天,被覆盖1/4;第47天,被覆盖l/8……依此类推,在第40天结束时,也就是青蛙们能够采取行动的最晚时间,池塘被睡莲覆盖1/1024。这就是一个系统思考的例子。虽然1/1024是一个非常非常小的数字———只是0.00098,不到千分之一。但它意味着,如果青蛙们想要避免陷入无处容身的危险境地,就必须在睡莲覆盖面积不到整个池塘的千分之一时就采取行动。如果池塘是一百平方米,千分之一也就几个巴掌大。也就是说,它们必须对在很远的地方发生的非常非常小的事情保持足够的警惕,并及时采取行动。如果它们在危险已经降临———比如,突然发现睡莲已经覆盖了池塘的四分之一甚至是十分之一——之前没有采取行动,那么,一切都晚了。 " j6 T* u. V/ o3 f4 Q
9 v! I9 m, a3 s% _, k, l7 V
. o" f5 |* E) o) m[書摘]系統思考:克服盲點、面對複雜性、見樹又見林的整體思考(Thinking in Systems: A Primer)
6 @8 U6 j4 d3 y r9 K9 thttps://blog.csdn.net/weixin_42008031/article/details/79968282& _; t: R* x. r+ c+ L6 y6 y
/ a. Q7 M* |4 c0 l1 E+ X1 B |
评分
-
2
查看全部评分
-
|